Showing posts with label Մաթեմատիկա. Show all posts
Showing posts with label Մաթեմատիկա. Show all posts
Tuesday, February 23, 2016
Thursday, January 28, 2016
Նախագիծ 4. Եռանկյունաչափության տարրեր
Դիտարկենք կոորդինատների սկզբնակետում կենտրոն և մեկ միավորի
հավասար շառավիղ ունեցող շրջանագիծ (միավոր շրջանագիծ): Միավոր
շրջանագծի վրա նշենք P0 (1;0) կետը (նկ.1): OP0
շառավիղը կոչվում է
սկզբնական շառավիղ:
 Եթե սկզբնական շառավիղը պտտվում է O կետի շուրջը ժամի սլաքի
ուղղությամբ, ապա պտտման անկյունը համարվում է բացասական, իսկ եթե
սկզբնական շառավիղ պտտվում է O կետի շուրջը ժամի սլաքին հակառակ,
ապա պտտման անկյունը համարվում է դրական: Սկզբնական շառավիղը O
կետի շուրջը α անկյունով պտտելիս P0 (1;0) կետը անցնում է Pα
կետ
Եթե սկզբնական շառավիղը պտտվում է O կետի շուրջը ժամի սլաքի
ուղղությամբ, ապա պտտման անկյունը համարվում է բացասական, իսկ եթե
սկզբնական շառավիղ պտտվում է O կետի շուրջը ժամի սլաքին հակառակ,
ապա պտտման անկյունը համարվում է դրական: Սկզբնական շառավիղը O
կետի շուրջը α անկյունով պտտելիս P0 (1;0) կետը անցնում է Pα
կետ
ին:
Բերման բանաձևեր
 Եթե սկզբնական շառավիղը պտտվում է O կետի շուրջը ժամի սլաքի
ուղղությամբ, ապա պտտման անկյունը համարվում է բացասական, իսկ եթե
սկզբնական շառավիղ պտտվում է O կետի շուրջը ժամի սլաքին հակառակ,
ապա պտտման անկյունը համարվում է դրական: Սկզբնական շառավիղը O
կետի շուրջը α անկյունով պտտելիս P0 (1;0) կետը անցնում է Pα
կետ
Եթե սկզբնական շառավիղը պտտվում է O կետի շուրջը ժամի սլաքի
ուղղությամբ, ապա պտտման անկյունը համարվում է բացասական, իսկ եթե
սկզբնական շառավիղ պտտվում է O կետի շուրջը ժամի սլաքին հակառակ,
ապա պտտման անկյունը համարվում է դրական: Սկզբնական շառավիղը O
կետի շուրջը α անկյունով պտտելիս P0 (1;0) կետը անցնում է Pα
կետին:
- Pα կետի օրդինատը կոչվում է α անկյան սինուս, իսկ աբսցիսը` α անկյան կոսինուս:
- α անկյան տանգենս է կոչվում α անկյան սինուսի հարաբերությունը կոսինուսին:
- α անկյան կոտանգենս է կոչվում α անկյան կոսինուսի հարաբերու- թյունը սինուսին:
- Մեկ ռադիանի անկյունը այն կենտրոնական անկյունն է, որը շրջա- նագծից անջատում է նրա շառավղին հավասար երկարությամբ աղեղ:
- 1 ռադ = 180 /π, 1*= 180/ π = ռադ, մասնավորապես` 180* = π ռադ.:
Եռանկյունաչափական հիմնական բանաձևերը
sin2x + cos2x = 1
tgx
|
=
|
sinx
|
cosx
|
ctgx
|
=
|
cosx
|
sinx
|
tgx ctgx = 1
tg2x + 1
|
=
|
1
|
cos2x
|
ctg2x + 1
|
=
|
1
|
sin2x
|
Բերման բանաձևեր
Նախագիծ 3. Լոգարիթմներ
Լոգարիթմ,  թվի լոգարիթմ
թվի լոգարիթմ  հիմքով, որտեղ
հիմքով, որտեղ  , կոչվում է այն թիվը, որով պետք է աստիճան բարձրացնել
, կոչվում է այն թիվը, որով պետք է աստիճան բարձրացնել  հիմքը
հիմքը  թիվը ստանալու համար։
թիվը ստանալու համար։
 թվի լոգարիթմ
թվի լոգարիթմ  հիմքով, որտեղ
հիմքով, որտեղ  , կոչվում է այն թիվը, որով պետք է աստիճան բարձրացնել
, կոչվում է այն թիվը, որով պետք է աստիճան բարձրացնել  հիմքը
հիմքը  թիվը ստանալու համար։
թիվը ստանալու համար։
Այն նշանակում են 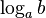 տեսքով և կարդում «լոգարիթմ
տեսքով և կարդում «լոգարիթմ  հիմքով
հիմքով  »։
»։
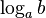 տեսքով և կարդում «լոգարիթմ
տեսքով և կարդում «լոգարիթմ  հիմքով
հիմքով  »։
»։
Սահմանումից հետևում է, որ  հավասարումը համարժեք է
հավասարումը համարժեք է  հավասարմանը Օր՝
հավասարմանը Օր՝  , քանի որ
, քանի որ 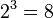 ։
։
 հավասարումը համարժեք է
հավասարումը համարժեք է  հավասարմանը Օր՝
հավասարմանը Օր՝  , քանի որ
, քանի որ 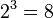 ։
։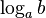 արտահայտությունը որոշված է այն և միայն այն դեպքում, երբ
արտահայտությունը որոշված է այն և միայն այն դեպքում, երբ 
Լայն կիրառություն ունեն հետևյալ տեսքի լոգարիթմները.
- Բնական. հիմքը հանդիսանում է Էյլերի թիվը (e).
- Տասնորդական.
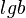 , հիմքը հանդիսանում է
, հիմքը հանդիսանում է  -ը.
-ը. - Երկուական.
 , հիմքը հանդիսանում է
, հիմքը հանդիսանում է  -ը։
-ը։
Սրանք լայն կիրառություն ունեն օրինակ ինֆորմատիկայում, շատ դիսկրետ մաթեմատիկական բաժանումներում և այլն։
Thursday, January 21, 2016
Երկրորդ նախագիծ «Իրական թվեր»
 Կոտորակները հնարավորություն են տալիս գրել ոչ ամբողջ թվերը։ Կոտորակներով կարելի է լրացնել ամբողջ թվերի միջև եղած միջակայքերը, իսկ դա հնարավորություն է տալիս ավելի ճշգրիտ չափումներ կատարել։ Կա կոտորակային թվերը գրելու 2 եղանակ. այսպես կոչված սովորական կոտորակներ, որը 2 ամբողջ թվերի հարաբերություն է, օրինակ՝ 3/4, և տասնորդական կոտորակներ, օրինակ՝ 0, 75։ Սովորական կոտորակի վերևի թիվն անվանում են համարիչ, ներքևինը՝ հայտարար։
Կոտորակները հնարավորություն են տալիս գրել ոչ ամբողջ թվերը։ Կոտորակներով կարելի է լրացնել ամբողջ թվերի միջև եղած միջակայքերը, իսկ դա հնարավորություն է տալիս ավելի ճշգրիտ չափումներ կատարել։ Կա կոտորակային թվերը գրելու 2 եղանակ. այսպես կոչված սովորական կոտորակներ, որը 2 ամբողջ թվերի հարաբերություն է, օրինակ՝ 3/4, և տասնորդական կոտորակներ, օրինակ՝ 0, 75։ Սովորական կոտորակի վերևի թիվն անվանում են համարիչ, ներքևինը՝ հայտարար։
Իսկ տասնորդական կոտորակը, օրինակ՝ 16, 25, գրվում է առանց հայտարարի և կարդացվում «տասնվեց ամբողջ քսանհինգ հարյուրերորդական»։ Տասնորդական կոտորակներում ինչպես ամբողջ թվերի, այնպես էլ ստորակետից հետո եղած թվերի արժեքը կախված է դրանց գրաված տեղից՝ կարգից. յուրաքանչյուր կարգ գնահատվում է 10 անգամ ավելի փոքր, քան ձախ կողմի հարևանը։ Այսպիսով` 16, 25 տասնորդական կոտորակում 2 թիվը նշանակում է 2 տասնորդական, իսկ 5-ը՝ 5 հարյուրերորդական. արդյունքում՝ քսանհինգ հարյուրերորդական։
Նույնհայտարարով երկու կոտորակներից մեծ է այն կոտորակը,որի համարիչը մեծ է:
Օր՝ 3/5>1/5
Եթե կոտորակիհամարիչն ու հայտարարը իրար հավասար են,կոտորակը հավասար է 1-ի:
Օր՝5/5=1
Տասնորդական կոտորակները կարող ենք կլորացնել մինչև միավորներ։ Եթե հատվածի վրա դասավորված երկու իրար հաջորդող բնական թվերի միջև գտնվող տասնորդական կոտորակի ստորակետից հետո գրված է 0, 1, 2, 3 կամ 4 թվանշանը, ուրեմն այն ավելի մոտ է իրենից ձախ ընկած բնական թվին։ Իսկ եթե երկու իրար հաջորդող բնական թվերի միջև գտնվող տասնորդական կոտորակի ստորակետից հետո գրված է 6, 7, 8 կամ 9 թվանշանը, ուրեմն այն ավելի մոտ է իրենից աջ ընկած բնական թվին։ Օրինակ, 18.7 թիվը գտնվում է 18-ի և 19-ի միջև, իսկ քանի որ ստորակետից հետո գրված է 7, ուրեմն 18.7 թիվը ավելի մոտ է 19-ին։ Նշանակում է՝ 18.7 թվի փոխարեն կգրենք 19։ 18.7 թվի փոխարինումը 19 թվով անվանում են այդ թվի կլորացում մինչև միավորները։Տասնորդական կոտորակները հարկ է լինում կլորացնել նաև մինչև մյուս կարգերը։ Տասնորդական կոտորակը մինչև որևէ կարգ կլորացնելիս այդ կարգին հաջորդող բոլոր , իսկ եթե նրանք ստորակետից հետո են, ապա դրանք անտեսում են։ Եթե այդ կարգին հաջորդող թվանշանը 5, 6, 7, 8 կամ 9 է, ապա վերջին պահպանվող թվանշանը մեծացնում են 1-ով։ Եթե այդ կարգին հաջորդող առաջին թվանշանը 0, 1, 2, 3 կամ 4 է, ապա վերջին պահպանվող թվանշանը չեն փոխում։Օրինակ 1. 75.3659-ը կլորացնենք մինչև տասնորդականները։ Անտեսենք տասնորդականներին հաջորդող բոլոր թվանշանները։ Անտեսվող թվանշաններից առաջինը 7 թվանշանն է, ուստի տասնորդականների կարգին ավելացնում ենք մեկ.
Տոկոսները կոտորակների հատուկ տեսակ են. «25 տոկոս» (գրվում է 25 %) բառը նշանակում է 25/100, այսինքն` մեկ քառորդ: 50 %-ը նույնն է, ինչ 50/100-ը, այսինքն՝ կեսը: Այսպիսով` տոկոսի նշանը (%) ցույց է տալիս, որ մենք գործ ունենք կոտորակի հետ, որի հայտարարը հավասար է 100-ի:Տոկոսների գրության եղանակը կիրառվում է, երբ հարկավոր է տեղեկություններ հաղորդել որևէ համամասնության վերաբերյալ: Օրինակ՝ եթե մենք հարցաշարի 100 հարցից ճիշտ ենք պատասխանում 70-ին, ապա կարելի է ասել, որ մեր գիտելիքների մակարդակը 70 % է: Տոկոսները հաճախ օգտագործում են աշխատավարձի կամ գների աճը ցույց տալու համար: Եթե սուրճի գինն աճում է 20 %-ով, ապա սրճարանում 200 դրամ արժեցող մեկ գավաթ սուրճը կթանկանա 200/20 դրամով, այսինքն՝ 40 դրամով, և կդառնա 240 դրամ:Երբ վաճառվում է հարկվող ապրանք, ապա հարկը սահմանվում է որոշակի տոկոսով, օրինակ` 25 % հարկը նշանակում է, որ ապրանքի հիմնական գնի յուրաքանչյուր 100 դրամի դիմաց մենք հարկադրված ենք վճարել 25 դրամ հարկ, և եթե ապրանքն արժե 100 դրամ, ապա հարկի հետ միասին այն կարժենա 125 դրամ:
Բացասական Թվեր
Երկու թվերից փոքր է համարվում այն, որի պատկերը կոորդինատային ուղղի վրա դասավորված է ավելի ձախ, և մեծ է համարվում այն, որի պատկերը դասավորված է ավելի աջ:
Կոորդինատային ուղղի վրա դրական թվերը պատկերվում են զրոյից աջ, իսկ բացասականները` զրոյից ձախ: Ուրեմն, յուրաքանխյուր դրական թիվ մեծ է զրոյից, իսկ յուրաքանչյուր բացասական թիվ փոքր է զրոյից, ուստի յուրաքանչյուր բացասական թիվ փոքր է յուրաքանչյուր դրական թվից:
Եթե ուղղի վրա նշենք երկու բացասական թվեր, ապա ավելի ձախ կգտնվի այն թիվը, որի բացարձակ մեծությունը մեծ է: Ուստի երկու բացասական թվերից փոքր է այն թիվը, որի բացարձակ մեծությունը մեծ է, և մեծ է այն, որի բացարձակ մեծությունը փոքր է:
2. 3)-1/60(առաջին և երկրորդ թվերը բերում ենք ընդհանուր հայտարարի՝180, ապա հանում ենք իրարից ցտանու ենք -3/180, կրճատում ենք 3-ով և ստանում -1/60:)
3.3) 47/380 (թվերը կրկին բերում ենք ընդհանուր հայտարարի այս անգամ գումարում ենք և բաժանում իրենց քանակին տվյալ պարագայում 2-ի)
4. 1) 2/15
1. 2)35
7x100/20=35
2. 3)7
19+9=28
28:4=7
3. 2)11
20,21,22,23,24,25,26,27,28,29,30:
4. 2)2
157x3 (թվի թվանշանները գումարում ենք իրար, ստացվում է 16: Եվ տեսնում ենք, թե տարբերակներից ո՞ր թվի գումարման դեպքում այն կբաժանվի 9-ի)
7x100/20=35
2. 3)7
19+9=28
28:4=7
3. 2)11
20,21,22,23,24,25,26,27,28,29,30:
4. 2)2
157x3 (թվի թվանշանները գումարում ենք իրար, ստացվում է 16: Եվ տեսնում ենք, թե տարբերակներից ո՞ր թվի գումարման դեպքում այն կբաժանվի 9-ի)
Sunday, September 27, 2015
Առաջին նախագիծ. «Բնական թվեր»
Այն թվերը, որոնք առաջացել են բնական ձևով առարկաների քանակը հաշվելիս (ինչպես հաշվարկման առումով, այնպես էլ համարակալման առումով)՝ կոչվում են բնական թվեր։
Բացասական և ոչ ամբողջ (ռացիոնալ, իրական, …) թվերը բնական թվեր չեն կարող լինել։ Բոլոր բնական թվերի բազմությունը ընդունված է նշանակել
N –ով:
Ցանկացած բնական թիվ կարելի է վերլուծել ըստ կարգերի, այսինքն ներկայացնել կարգային գումարելիների գումարի տեսքով,
օրինակ`
5789=5·1000 + 7·100 + 8·10 + 9
Թվերի վերլուծումն ըստ
կարգերի կարելի է կիրառել նաև բազմանիշ տվեր գումարելիս, օրինակ գումարենք 564 և
782 թվերը:
564+782 = (500+60+4)+
(700+80+2)
Կիրառելով գումարման
զուգորդական և տեղափոխական օրենքները, ստանում ենք`
564+782 = (500+60+4)
+ (700+80+2) = (500+700) + (60+80)
+ (4+2) = 1200 + 140 + 6
Կարգային միավորները
կարելի է գրել նաև 10 թվի բնական ցուցիչով աստիճաննեի գումարի տեքով, օրինակ՝
5789 = 5·103+7·102+8·101+9·100
Թվաբանական գործողություններ բնական թվերով, դրանց
հատկությունները
Մաթեմատիկայում թվաբանական
գործողություները 4-ն են՝ գումարում, հանում, բազմապատկում, բաժանում:
Գումարում՝
45+82=127
503+968=1471
Հանում՝
5023-4792=231
92-64=28
Բազմապատկում՝
87·95= 8265
62·24= 1488
Բաժանում՝
714 : 21= 34
312 : 6= 52
Թվաբանական գործողությունների հատկություններին
են՝
Գումարելիների
տեղերը փոխելիս գումարը
մնում է անփոփոխ։
Հանելիի ու տարբերության
գումարը հավասար է նվազելիին։
Արտադրիչների
տեղերը փոխելիս արտադրյալը
մնում է անփոփոխ։
Բաժանարարի ու քանորդի
արտադրյալը հավասար է բաժանելիին։
Պարզ և բաղադրյալ թվեր
Բնական թվերը կարող
են լինել պարզ
և բաղադրյալ։ Պարզ
են կոչվում այն
թվերը, որոնք ունեն
միայն երկու բաժանարար՝
1-ը և տվյալ թիվը։
Օրինակ՝ 2, 3, 5, 7, 11,13 ,17...:
2-ը միակ զույգ
պարզ թիվն է։
Երեք և ավելի
բաժանարար ունեցող թվերը կոչվում
են բաղադրյալ։ Բացառություն
է համարվում՝ 1 թիվը, որը ունի
միայ մեկ բաժանարար՝
1-ը, այն նույնպես համարվում է բաղադրյալ
թիվ։
Բաժանման հայտանիշներ
2-ի բաժանվում
են 0, 2, 4, 6, կամ 8 թվանշաններով վերջացող բոլոր
թվերը։ Այդ
թվերը կոչվում
են զույգ։
Թիվը բաժանվում է
3-ի, եթե
նրա թվանշանների
գումարը բաժանվում
է 3-ի։
Թիվը բաժանվում է
4-ի եթե
նրա վերջին
2 թվանշաններով կազմված
թիվը բաժանվում
է 4-ի,
կամ դրանք
0-ներ են։
5-ի բաժանվում
են միայն
0-ով կամ
5-ով վերջացող
թվերը։
6-ի բաժանվում
են 3-ի
բաժանվող զույգ
թվերը։
Թիվը բաժանվում է 8-ի եթե նրա
վերջին 3 թվանշաններով կազմված թիվը
բաժանվում է 8-ի,
կամ դրանք 0-ներ
են։
Թիվը բաժանվում է 9-ի,
եթե նրա թվանշանների
գումարը բաժանվում է 9-ի։
Ամենամեծ ընդհանուր բաժանարար և ամենափոքր ընդհանուր
բազմապատիկ
Երկու բնական թվերի ամենամեծ
ընդհանուր բաժանարար է կոչվում
այն ամենամեծ բնական
թիվը, որին բաժանվում
են տրված 2 թվերը
անմնացորդ։
Երկու թվերի ամենամեծ
ընդհանուր բաժանարարը գտնելու համար անհրաժեշտ է՝
1. թվերը վերլուծել
պարզ արտադրիչների ,
2. ստացած վերլուծումներում
գտնել բոլոր ընդհանուր պարզ արտադրիչները,
3. հաշվել բոլոր ընդհանուր
պարզ արտադրիչների արտադրյալը:
Օրինակ՝ 36 և 54-ը
36= 2·2·3·3 54= 2·3·3·3
2·3·3=18
18-ը 36 և 54 թվերի
ամենամեծ ընդհանուր բաժանարարն է:
Երկու բնական թվերի ամենափոքր
ընդհանուր բազմապատիկ է կոչվում
այն ամենափոքր բնական
թիվը, որը բաժանվում
է տրված 2 թվերին
անմնացորդ։
1. թվերը վերլուծել պարզ արտադրիչների ,
2. այդ թվերից որևէ
մեկի վերլուծումը լրացնել մյուսի այն արտադրիչներով, որոնք չկան առաջին թվի վերլուծման
մեջ,
3. հաշվել ստացված արտադրյալը:
Օրինակ՝18 և 24 թվերը:
24 = 2 ⋅ 2 ⋅
2 ⋅ 3 18 = 2 ⋅ 3 ⋅
3
2 ⋅ 3 ⋅
3 ⋅ 2 ⋅ 2 = 72
72-ը 18 և 24 թվերի ամենափոքր ընդհանուր բազմապատիկն է:
Շտեմարանային օրինակներ՝
1.
Հետևելով բաժանման հայտանիշից (թիվը բաժանվում է 9-ի, եթե նրա թվանշանների գումարը բաժանվում է 9-ի), ապա ճիշտ պատասխանն է 2)-ը, քանի որ 2+9+6+1+0=18, իսկ 18/6= 2
2.

Տրված բառերի ամենամեծ ընդհանուր բաժանարար է համարվում՝ 4)8-ը
3.

Ճիշտ պատասխանն է 3)90-ը
4.
1/ ամենափոքր ընդհանուր բազմապատիկն է 36-ը (12*3=36;18*2=36)
2/12+18=30
30/2=15
Պատասխանն է ՝2)15:
3/-12+18=6
Պատասխանն է `4)6:
4/12*18=216
216=6*6*6
Պատասխանն է `1)6
Շտեմարանային օրինակներ՝
1.
Հետևելով բաժանման հայտանիշից (թիվը բաժանվում է 9-ի, եթե նրա թվանշանների գումարը բաժանվում է 9-ի), ապա ճիշտ պատասխանն է 2)-ը, քանի որ 2+9+6+1+0=18, իսկ 18/6= 2
2.
Տրված բառերի ամենամեծ ընդհանուր բաժանարար է համարվում՝ 4)8-ը
3.
Ճիշտ պատասխանն է 3)90-ը
4.
1/ ամենափոքր ընդհանուր բազմապատիկն է 36-ը (12*3=36;18*2=36)
2/12+18=30
30/2=15
Պատասխանն է ՝2)15:
3/-12+18=6
Պատասխանն է `4)6:
4/12*18=216
216=6*6*6
Պատասխանն է `1)6
Monday, May 4, 2015
Առաջադրանք 4
Գծել լոգարիթմական ֆունկցիայի գրաֆիկ և դրանից օգտվելով թվարկել ֆունկցիայի բնութագրիչները: Պարզագույն լոգարիթմական հավասարումների և անհավասարումների լուծելը:
 Լոգարիթմական ֆունկցիա կոչվում է f (x) = log a = x, որտեղ a-ն 1- ից տարբեր դրական թիվ է:
1)Ֆունկցիայի որոշման տիրույթը դրական կիսառանցքն է՝
D(f)=(0,∞):
2)Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է՝
E(f)=(− ∞,∞):
3)Ֆունկցիան մոնոտոն է իր որոշման տիրույթում: Ընդ որում այն աճող է, եթե ՝ a > 1, և նվազող՝ եթե 0 < a <1:
4)Ֆունկցիան 0 արժեքն ընդունում է x=1 կետում:
5)ա) a > 1 դեպքում ֆունկցիան բացասական է (0,1) և դրական ( 1,∞) միջակայքերում:
բ) 0 < a < 1 դեպքում ֆունկցիան դրական է (0,1) և դրական ( 1,∞) միջակայքերում:
Լոգարիթմական ֆունկցիա կոչվում է f (x) = log a = x, որտեղ a-ն 1- ից տարբեր դրական թիվ է:
1)Ֆունկցիայի որոշման տիրույթը դրական կիսառանցքն է՝
D(f)=(0,∞):
2)Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է՝
E(f)=(− ∞,∞):
3)Ֆունկցիան մոնոտոն է իր որոշման տիրույթում: Ընդ որում այն աճող է, եթե ՝ a > 1, և նվազող՝ եթե 0 < a <1:
4)Ֆունկցիան 0 արժեքն ընդունում է x=1 կետում:
5)ա) a > 1 դեպքում ֆունկցիան բացասական է (0,1) և դրական ( 1,∞) միջակայքերում:
բ) 0 < a < 1 դեպքում ֆունկցիան դրական է (0,1) և դրական ( 1,∞) միջակայքերում:
Լոգարիթմի հիմնական հատկությունները
 Լոգարիթմական ֆունկցիա կոչվում է f (x) = log a = x, որտեղ a-ն 1- ից տարբեր դրական թիվ է:
1)Ֆունկցիայի որոշման տիրույթը դրական կիսառանցքն է՝
D(f)=(0,∞):
2)Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է՝
E(f)=(− ∞,∞):
3)Ֆունկցիան մոնոտոն է իր որոշման տիրույթում: Ընդ որում այն աճող է, եթե ՝ a > 1, և նվազող՝ եթե 0 < a <1:
4)Ֆունկցիան 0 արժեքն ընդունում է x=1 կետում:
5)ա) a > 1 դեպքում ֆունկցիան բացասական է (0,1) և դրական ( 1,∞) միջակայքերում:
բ) 0 < a < 1 դեպքում ֆունկցիան դրական է (0,1) և դրական ( 1,∞) միջակայքերում:
Լոգարիթմական ֆունկցիա կոչվում է f (x) = log a = x, որտեղ a-ն 1- ից տարբեր դրական թիվ է:
1)Ֆունկցիայի որոշման տիրույթը դրական կիսառանցքն է՝
D(f)=(0,∞):
2)Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է՝
E(f)=(− ∞,∞):
3)Ֆունկցիան մոնոտոն է իր որոշման տիրույթում: Ընդ որում այն աճող է, եթե ՝ a > 1, և նվազող՝ եթե 0 < a <1:
4)Ֆունկցիան 0 արժեքն ընդունում է x=1 կետում:
5)ա) a > 1 դեպքում ֆունկցիան բացասական է (0,1) և դրական ( 1,∞) միջակայքերում:
բ) 0 < a < 1 դեպքում ֆունկցիան դրական է (0,1) և դրական ( 1,∞) միջակայքերում:
Log48=log2223=3/2
Log525=log552=2
Lg25+lg4=lg100=lg102=2
Log334=4log33=4
Thursday, April 9, 2015
Առաջադրանք 5:
GeoGebra ծրագրով գծեք միավոր շրջանագիծ: Օգտվելով գծագրից հինգ տարբեր անկյունների համար գտեք դրանց սինուսը և կոսինուսը: Գտած անկյունների համար ստուգեք եռանկյունաչափական հիմնական նույնությունը:

Sin45=0,71
Cos45=0,71


Sin30=0,5
Cos30=0,87
Sin60=0,87

Sin35=0,57
Sin15=0.26
Cos15=0.97
Sin2α+cos2 α=1
Sin45=0,71
Cos45=0,71

Sin30=0,5
Cos30=0,87
Sin60=0,87
Cos60=0,5
Sin35=0,57
Cos35=0.82
Sin15=0.26
Cos15=0.97
Sin2α+cos2 α=1
Sin230+cos230=1
1-sin230=cos230
1-0.25=0.75
Cos2=0.75
Cos=0.87
Thursday, January 29, 2015
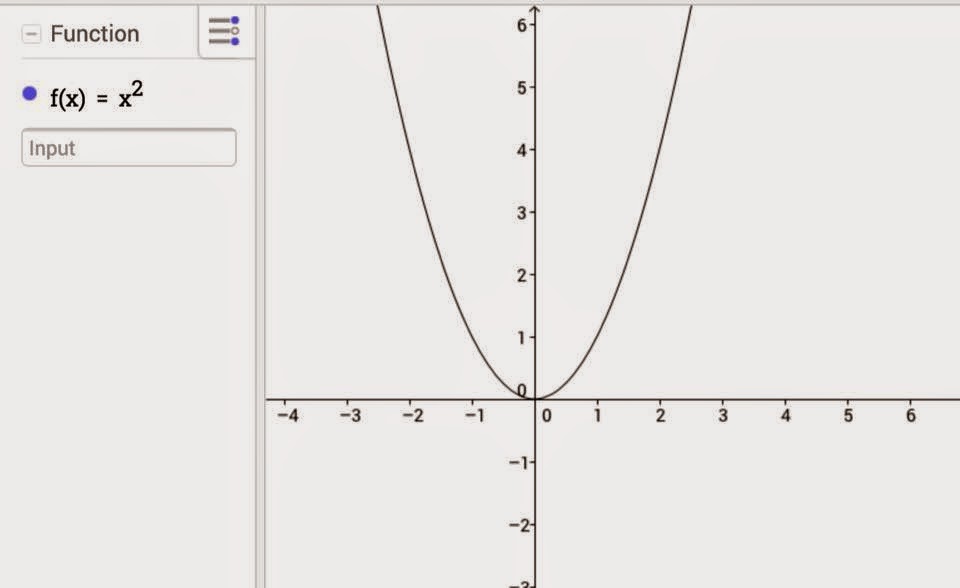
Աստիճանային Ֆունկցիա
Աստիճանային ֆունկցիա կոչվում է f (x)=x^a բանաձևով տրված ֆունկցիան, որտեղ a-ն բացի զրոյից ցանկացած թիվ է:
Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է E (f)=(-∞; +∞), որովհետև ֆունկցիան ընդունում է ցանկացած կամայականիրական արժեք: Հետևաբար` ֆունկցիան անսահմանափակ է և չունիմեծագույն ու փոքրագույն արժեքներ:
Բնական ցուցիչով աստիճանային ֆունկցիան իր շատ հատկություններովնման է գծային ֆունկցիային, երբ n-կենտ է, և քառակուսայինֆունկցիային, երբ n-ը զույգ է:
Ուսումնասիրենք f (x)=x^n ֆունկցիայի հատկություններն այն դեպքում, երբ n-ը կենտ է:
D (f)=(-∞; +∞)
Ֆունկցիան կենտ է, քանիոր կենտ n-ի դեպքում f (-x)=(-x)^n=-x^n=-f (x)
Ֆունկցիան ունի մեկ զրո` f (0)=0
Ֆունկցան դրական է, երբx € (0; +∞), և բացասականէ, երբ x € (-∞; 0)
Եթե n-ը կենտ է, ապաֆունկցիայի գրաֆիկըգտնվում է առաջին ևերրորդ քառորդներում: Ֆունկցիայի որոշման տիրույթն ամբողջ թվայինառանցքն է D (f)=(-∞;+∞)
| Ֆունկցիան աճում է ամբողջ թվային առանցքի վրա: |
Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է E (f)=(-∞; +∞), որովհետև ֆունկցիան ընդունում է ցանկացած կամայականիրական արժեք: Հետևաբար` ֆունկցիան անսահմանափակ է և չունիմեծագույն ու փոքրագույն արժեքներ:
Ուսումնասիրենք f (x)=x^n ֆունկցիայի հատկություններն այնդեպքում, երբ n-ը զույգ է:
Ֆունկցիայի որոշմանտիրույթն ամբողջովինթվային առանցքն է:
D (f)=(-∞; +∞)
Ֆունկցիան զույգ է, որովհետևf (-x)=(-x)^n=x^n=f (x)
Ֆունկցիան ունի մեկ 0, f (0)=0
Ֆունկցիան դրական է, երբ x0, և ֆունկցիայի գրաֆիկըգտնվում է առաջին ուերկրորդ քառորդներում:
Ֆունկցիան աճում է (-∞;0] միջակայքում և աճում [0;+∞) միջակայքում:
Ֆունկցիայի փոքրագույնարժեքը 0-ն է, որըֆունկցիան ընդունում է x=0 կետում:
Ֆունկցիան չունիմեծագույն արժեք:
Ֆունկցիայի արժեքներիբազմությունը ոչբացասական թվերիբազմությունն է` E (f)=[0; +∞)
Subscribe to:
Posts (Atom)