Աստիճանային Ֆունկցիա

Աստիճանային ֆունկցիա կոչվում է f (x)=x^a բանաձևով տրված ֆունկցիան, որտեղ a-ն բացի զրոյից ցանկացած թիվ է:

Բնական ցուցիչով աստիճանային ֆունկցիան իր շատ հատկություններովնման է գծային ֆունկցիային, երբ n-կենտ է, և քառակուսայինֆունկցիային, երբ n-ը զույգ է:

 Ուսումնասիրենք f (x)=x^n ֆունկցիայի հատկություններն այն դեպքում, երբ n-ը կենտ է:

Ֆունկցիայի որոշմանտիրույթն ամբողջովինթվային առանցքն է:

 D (f)=(-∞; +∞)

Ֆունկցիան կենտ է, քանիոր կենտ n-ի դեպքում   f (-x)=(-x)^n=-x^n=-f (x)

Ֆունկցիան ունի մեկ զրո` f (0)=0

Ֆունկցան դրական է, երբx € (0; +∞), և բացասականէ, երբ x € (-∞; 0)

Եթե n-ը կենտ է, ապաֆունկցիայի գրաֆիկըգտնվում է առաջին ևերրորդ քառորդներում: Ֆունկցիայի որոշման տիրույթն ամբողջ թվայինառանցքն է D (f)=(-∞;+∞)

Ֆունկցիան աճում է ամբողջ թվային առանցքի վրա:

Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է E (f)=(-∞; +∞), որովհետև ֆունկցիան ընդունում է ցանկացած կամայականիրական արժեք: Հետևաբար` ֆունկցիան անսահմանափակ է և չունիմեծագույն ու փոքրագույն արժեքներ:

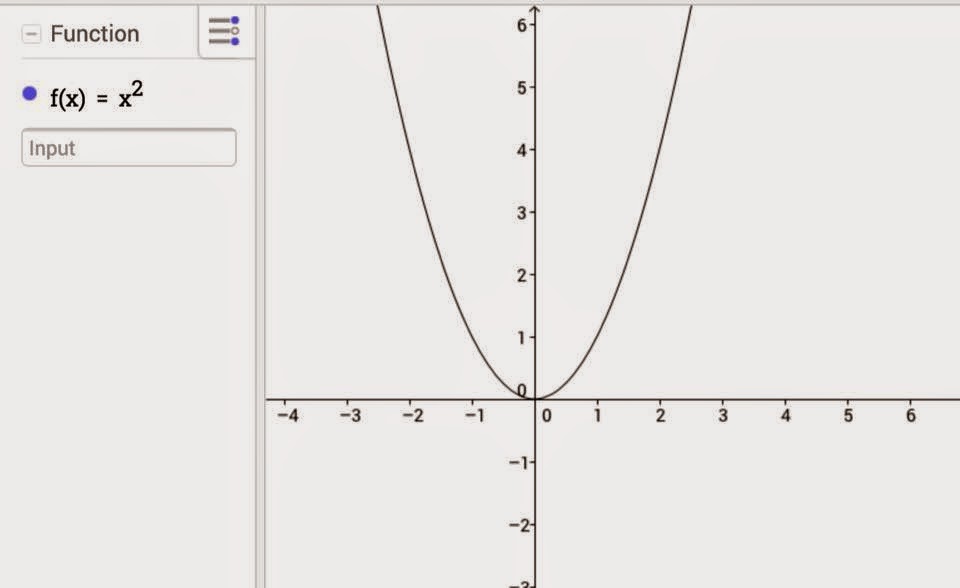
Ուսումնասիրենք f (x)=x^n ֆունկցիայի հատկություններն այնդեպքում, երբ n-ը զույգ է:

Ֆունկցիայի որոշմանտիրույթն ամբողջովինթվային առանցքն է:

D (f)=(-∞; +∞)

Ֆունկցիան զույգ է, որովհետևf (-x)=(-x)^n=x^n=f (x)

Ֆունկցիան ունի մեկ 0, f (0)=0

Ֆունկցիան դրական է, երբ x0, և ֆունկցիայի գրաֆիկըգտնվում է առաջին ուերկրորդ քառորդներում: 

Ֆունկցիան աճում է (-∞;0] միջակայքում և աճում  [0;+∞) միջակայքում:

Ֆունկցիայի փոքրագույնարժեքը 0-ն է, որըֆունկցիան ընդունում է x=0 կետում: 

Ֆունկցիան չունիմեծագույն արժեք:

Ֆունկցիայի արժեքներիբազմությունը ոչբացասական թվերիբազմությունն է` E (f)=[0; +∞)